История (Гиперболоид и Параболоид)

Гиперболоидную форму конструкций ввёл в архитектуру В. Г. Шухов (патент Российской Империи № 1896; от 12 марта 1899 года, заявленный В. Г. Шуховым 11.01.1896). Первая в мире стальная сетчатая башня в форме гиперболоида вращения была построена Шуховым для крупнейшей дореволюционной Всероссийской промышленной и художественной выставки в Нижнем Новгороде, проходившей с 28 мая (9 июня) по 1 (13) октября 1896 года.

Однополостный гиперболоид вращения первой башни Шухова образован 80 прямыми стальными профилями, концы которых крепятся к кольцевым основаниям. Сетчатая стальная оболочка из ромбовидно пересекающихся профилей упрочнена 8 параллельными стальными кольцами, расположенными между основаниями. Высота гиперболоидной оболочки башни — 25,2 метра (без учёта высот фундамента, резервуара и надстройки для обозрения).

Диаметр нижнего кольцевого основания — 10,9 метра, верхнего — 4,2 метра. Максимальный диаметр бака — 6,5 метра, высота — 4,8 метра. От уровня земли из центра основания башни до уровня дна резервуара поднимается красивая стальная винтовая лестница. В центральной части бак имеет цилиндический проход с прямой лестницей, ведущей на смотровую площадку на верхней поверхности резервуара.

Над смотровой площадкой на баке сделана гиперболоидная надстройка с прямой лёгкой лестницей, ведущей на более высокую малую смотровую площадку. Гиперболоидная надстройка смонтирована из 8 прямых профилей, упирающихся в кольцевые основания, между которыми расположено ещё одно упрочняющее кольцо. Верхняя площадка в 1896 году имела деревянный настил и ограждение (не сохранились до настоящего времени). Общая высота башни составляет 37 метров. Все стальные элементы конструкции башни соединены заклёпками.

После выставки первая башня Шухова была перенесена в имение мецената Ю. С. Нечаева-Мальцова в село Полибино Данковского района Липецкой области. Башня сохранилась до нашего времени, является памятником архитектуры, охраняется государством. Первая в мире гиперболоидная конструкция страдает от коррозии и нуждается в реставрации.

В начале 20-го века многие боевые корабли, в основном в США, строились с ажурными гиперболоидными мачтами.

Такое решение объясняется необходимостью размещения большого объёма наблюдательных и дальномерных приборов на большой высоте от палубы, меньшей уязвимостью в бою и амортизацией ударов от отдачи собственных, очень мощных, орудий.

Дальнейшей модификацией идеи сетчатых гиперболоидных конструкций стала конструкция радиобашни на Шаболовке в Москве, построенной Шуховым в 1919—1922 гг. Первоначальный проект высотой 350 м из-за дефицита металла был заменен на 150-метровый вариант, который эксплуатируется и поныне. В течение своей жизни Шухов построил более двухсот гиперболоидных башен различного назначения.

Гиперболоидные конструкции впоследствии строили многие великие архитекторы: Гауди, Ле Корбюзье, Оскар Нимейер.

Гиперболоидные шуховские башни востребованы и в настоящее время. В 1963 году в порту города Кобе в Японии по проекту компании Nikken Sekkei (недоступная ссылка) была построена 108-метровая гиперболоидная шуховская башня (Kobe Port Tower).

А в 1968 году в Чехии по проекту архитектора Карела Хубачека была построена гиперболидная башня «Йештед» высотой 100 метров. В 2003 году была построена гиперболоидная башня Шухова в Цюрихе. Авторы башни — архитекторы Даниэль Рот и Александр Ком (Daniel Roth, Alexander Kohm). Идеи гиперболоидных конструкций башен Шухова известный архитектор Михаил Посохин предложил использовать при проектировании новых небоскрёбов в деловом центре «Москва-Сити».

600-метровая гиперболоидная сетчатая шуховская башня построена в 2010 году в Гуанчжоу в Китае компанией Arup. На 2017 год это вторая по высоте башня в мире.

Гиперболоид

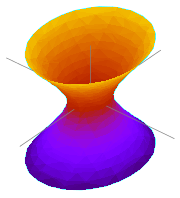
В математике гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

где a и b — действительные полуоси, а c — мнимая полуось;

или

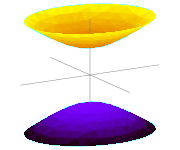
где a и b — мнимые полуоси, а c — действительная полуось.

Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двуполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: | AP — BP | = const

В этом случае A и B называются фокусами гиперболоида.

Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

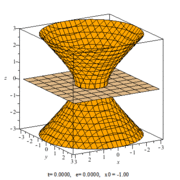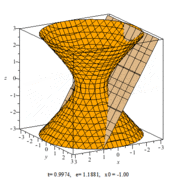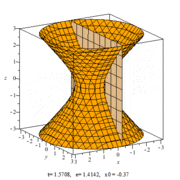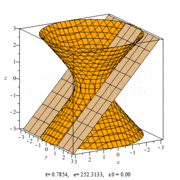
В сечении однополостного гиперболоида плоскостью можно получить кривую любого эксцентриситета (e) от нуля до бесконечности.

Параболоид

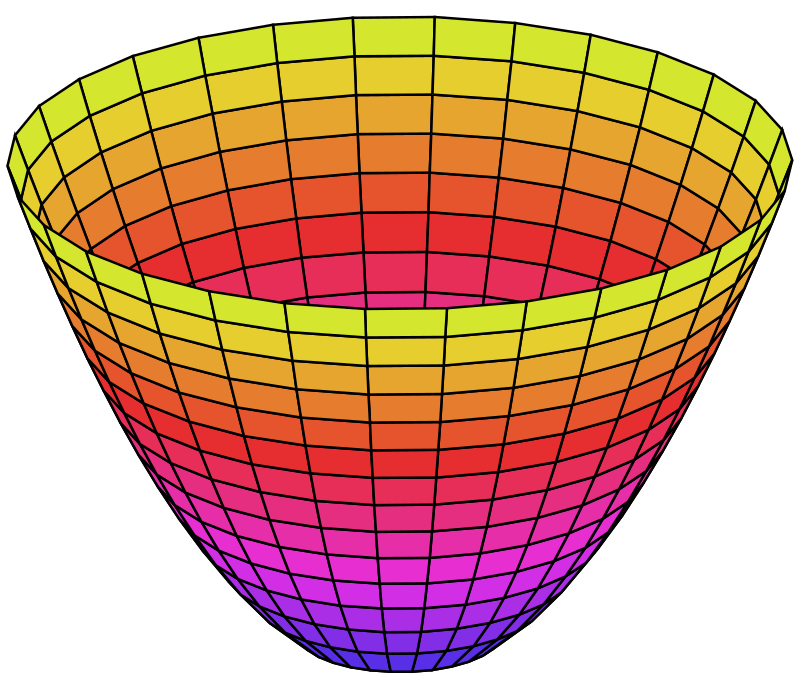
Параболо́ид ― тип поверхности второго порядка в трёхмерном евклидовом пространстве.

Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

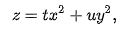
где t и u — действительные числа не равные нулю одновременно.

При этом:

если t и u одного знака, то параболоид называется эллиптическим, частный случай эллиптического параболоида t = u в этом случае поверхность принято называть параболоидом вращения;
Далее, если t и u разного знака, то параболоид называется гиперболическим;
если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.
Cечения параболоида вертикальными (параллельными оси z) плоскостями произвольного положения — параболы.

Сечения параболоида горизонтальными плоскостями, параллельными плоскости x\ y для эллиптического параболоида — эллипсы, для параболоида вращения эти пересечения — окружности, когда такое пересечение существует.

Пересечения для гиперболического параболоида — гиперболы.

В частных случаях пересечения, сечением может оказаться прямая или пара прямых (для гиперболического параболоида или пара параллельных прямых для параболического цилиндра) или вырождаться в одну точку (для эллиптического параболоида).

Материал из Википедии — свободной энциклопедии.